Pentagonal Pyramid Surface Area With Slant Height | A regular pentagonal pyramid with the length of an edge of 5 cm and a lateral area of 150 cm2? 1) find the surface area with a base length of 5centimeter, apothem length of 4centimeter and a slant height of 9centimeter. What is the surface area of this pentagonal pyramid? A, distance from center to midpoint of a side. Before we get started, let's review what a pyramid is.
A regular pentagonal pyramid with the length of an edge of 5 cm and a lateral area of 150 cm2? • surface area of pentagonal and hexagonal pyramids. To calculate this, you must find the areas of the triangular if you are not given the slant height of the pyramid, you must find it by considering the various triangles that exist within the solid. Multiply the perimeter by the slant length and divide by 2. Knowing the altitude and the slant height can give us enough information to calculate everything we need.
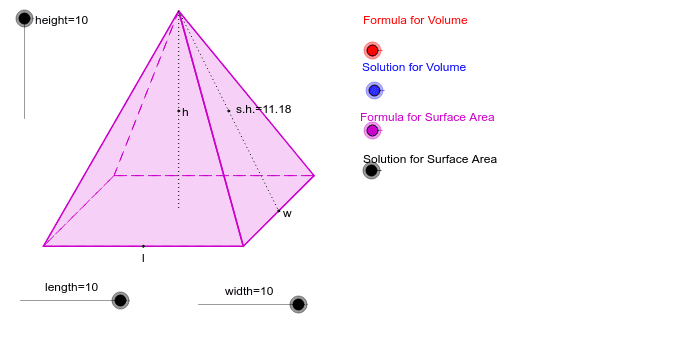
What is the surface area of this pentagonal pyramid? If this was a regular pentagonal pyramid, the slant height (length from the apex to the middle of one of the triangular faces) would be equal to (√3/2) times since the slant height is given, the surface area of the triangular faces is easy to find, with each triangular face having an area of (1/2)bh, or (1/2). With the slant height, now we can find the lateral area. If is the area of the base, and is the number of. Solved examples on surface area of pyramid. The pythagorean theorwm show the slant height to be 8. Regular pentagonal pyramid surface area you can get the surface area of a regular pentagonal pyramid using an equation with three variables. Each of height and side of the base of a regular hexagonal pyramid is equal to xcm. This is because the side faces are always triangles and the triangle formula is base times height divided by 2. To do this we start by using pythagoras to find the slant height. B, length of a side of the pentagonal base. Enter the slant height =. Knowing the slant height helps because it represents the height of the triangle that makes up each lateral face.
It is not for no reason this height is called slant height! What is the surface area of this pentagonal pyramid? This is because the side faces are always triangles and the triangle formula is base times height divided by 2. 1) find the surface area with a base length of 5centimeter, apothem length of 4centimeter and a slant height of 9centimeter. The surface area of a pyramid.

The word slant refers also to something that is oblique, bent, or something that is not vertical or straight up. Area of base(a) = (5/2)as surface area of pyramid = (5/2)as + (5/2)sl = a + (5/2)sl volume of pyramid = (5/6)abh. Slant height the slant height of a regular right pyramid is the line segment joining the vertex t. But in the particular case of a right square pyramid with the base side and slant height given, the area is given by the formula. This is because the side faces are always triangles and the triangle formula is base times height divided by 2. Animated demonstration of the pyramid surface area calculation. Surface area of square pyramid = b2 + 2bs where b is the length of the base and s is the slant height. A regular pentagonal pyramid with the length of an edge of 5 cm and a lateral area of 150 cm2? Pentagonal pyramid is a pyramid with a pentagonal base. Find the lateral area of a regular pentagonal pyramid that has a slant height of 14 in. You can get the surface area of a regular pentagonal pyramid using an equation with three variables. base area + 1 / 2 × perimeter × slant length. If this was a regular pentagonal pyramid, the slant height (length from the apex to the middle of one of the triangular faces) would be equal to (√3/2) times since the slant height is given, the surface area of the triangular faces is easy to find, with each triangular face having an area of (1/2)bh, or (1/2).
Surface area of a regular pyramid: But in the particular case of a right square pyramid with the base side and slant height given, the area is given by the formula. B, length of a side of the pentagonal base. Calculate the volume of square pyramids calculate the volume of prisms & pyramids. Find the lateral area of a regular pentagonal pyramid that has a slant height of 14 in.
Surface area of a pentagonal pyramid. Knowing the slant height helps because it represents the height of the triangle that makes up each lateral face. Knowing the altitude and the slant height can give us enough information to calculate everything we need. Each of height and side of the base of a regular hexagonal pyramid is equal to xcm. The area of each lateral face is 1/2 (12)(8), or 48, so l.a. For pyramids, we will need to use the slant height, which is labeled , to find the area of each triangular face. Learn how to compute the surface area of a square pyramid. The lesson is crystal clear and right to the point. Calculate the volume of square pyramids calculate the volume of prisms & pyramids. When all side faces are the same: base area + 1 / 2 × perimeter × slant length. For a pentagonal pyramid, the lateral area is the combined area of the five triangular sides of the pyramid. Regular triangular pyramid area of base : ½as surface area of pyramid : ½as + (3/2)sl volume of pyramid : (1/6)abh .
Find the surface area and volume of a pentagonal pyramid with the given apothem length 2, side 3, height 4 and the slant height 5 pentagonal pyramid surface area. Area of base(a) = (5/2)as surface area of pyramid = (5/2)as + (5/2)sl = a + (5/2)sl volume of pyramid = (5/6)abh.
Pentagonal Pyramid Surface Area With Slant Height: When all side faces are the same:
0 comments:
Post a Comment